|
The equation of separation for two dimensions of space was not ascribed to Pythagoras until sometime after
his death, and it is probable that he learned it during his visit to India, along with the pitch ratios of the
strings of the Kithara.
Suppose two ships' captains wish to measure the distance between two islands which have an impassable reef between
them. Suppose the first captain sails due north (by the stars) from one island until he sees the second island
directly to his right (east). He has then simply to sail to his right until he reaches the island. Then, knowing
the distance north that he sailed, and the distance east, by the use of Pythagoras' equation he can find the distance
between the islands without having to cross the reef.
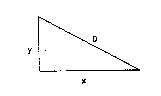
Suppose now that the second captain sails not due north by the stars, but sets his course by magnetic compass and
sails magnetic north until he sees the other island directly to his right (not directly east). If, then, he sails
directly to the island and knows the distances that his ship has moved, he, too, by the same equation, can calculate
the distance between the islands. This distance is said to be objective. Although the two captains chose different
coordinate systems and differed in their estimates of how far north and east the second island was, they agree
on the total distance between the islands. (However, it can easily be shown that this method of measurement and
calculation does not give the objective distance between the islands. Pythagoras' equation is applicable only to
a flat surface, a plane, but the surface of the Earth is curved. If the islands are several thousand miles apart,
it becomes a three-dimensional problem.)
But the world is not objective in three dimensions either. We live in a universe of four dimensions and, as Einstein
pointed out in 1905, time also must come into this equation if the equation is to remain invariant for observers
moving with respect to each other. Our problem is not how to measure from the southeast corner at the floor to
the northwest corner at the ceiling but, rather, how to measure the total separation, the four- dimensional separation,
between an event at one of those corners and another event at the other.
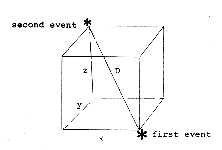
Our difficulty arises because the distance alone turns out not to be objective.
That is, two people moving with respect to each other measure different distances between those events. Also, the
time separation between two such events is not objective. Observers moving with respect to each other disagree
on the length of time that has elapsed between the two events. Only four-dimensional addresses such as here-now
or there-then are objective, and the separation between any two such addresses (events) is also objective.
Here, "moving with respect to each other" corresponds to our two ships' captains choosing different coordinate
systems, i.e., choosing different directions along which to measure north and east. Just as our ships' captains
differed in their estimates of the distances north and east to the second island, just so two observers moving
with respect to each other might differ in their estimates of the space and time separations between two events.
But just as our ships' captains agreed on the total distance between the islands, just so our two observers, moving
with respect to each other, will agree on the total separation between any two events. It is the same for all observers
regardless of their motion or their points of view. (Einstein never liked the term relativity theory. He wanted
it called the theory of invariants.)
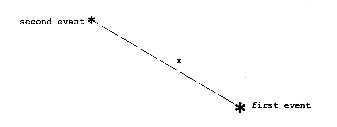
This, then, is our new geometry designed to save the objectivity of the universe. But does it? Between the events
here-now and there-then, one observer will see a greater distance between here and there and a greater time between
now and then. It is only the total separation, that is objective, or invariant.
Suppose that, standing here on Earth, we see two space ships approaching, one from the right and one from the left,
in opposite directions. Let us suppose that, as seen by us, each of them will pass our position at 99% of the speed
of light, one from right to left and one from left to right so that they pass very close to each other. Seen from
our ordinary understanding of space and time, we would say that the space ships will pass, that is the passengers
in each ship will see the other ship passing by, at 99 + 99 or l98% of the speed of light. But that is wrong. Our
ordinary understanding of space and time is wrong. We know from our measurements of physics that particles never
interact as if they were passing at speeds greater than or equal to the speed of light. We know from our measurements
of high-speed particles that the passengers of each space ship would see the other ship passing by at 99.995% of
the speed of light. Each of us will see the other's time measurements as "wrong" and the other's space
measurements, in the direction of the motion, as "wrong, " but we will all agree on the total separation
between any two events both of which can be seen from all three positions. With the help of our new geometry, our
fourdimensional geometry, we can understand the relationship of our several points of view so that we can still
see both events as objective and the separation between the two events as also objective.
Under what conditions is it true that the total separation will be zero? Is it simply a trivial case? No, it is
by no means trivial, because it is true for any two events one of which can be seen from the other. If what we
call a light beam can go from the event there-then to the event here-now, or from here-now to there-then, then
the events must be considered to be adjacent, that is, the total separation between them must be zero. It is true
for every event of our perception. The separation between the event of perception and the event perceived is zero.
We see the whole universe in the past. We cannot see anything when it happens. We can't see the backs of our hands
now. We see everything late. Every event that we see as away from us in space we see backwards in time, and it
is only on the basis of such perceptions, where the separation between the perceiver and the perceived is zero,
that we have come to the conclusion in the first place that the universe exists outside.
The ancients used to say that "the mind goes out through the eye and takes the form of a pot." The moderns
say that "the photons come in from the pot and take a form in the eye. " The equation says that it makes
no difference which mistake we make — the separation is zero. In an effort to save the objectivity of the universe,
we have had to abandon the separation between the perceiver and the perceived.
The universe which we see is set up in this very peculiar way so that we cannot see anything when it happens. We
see the whole show in the past. If we see an event in the Andromeda Galaxy at a distance of two and a quarter million
light years from us, we see it two and a quarter million years ago. Why? Usually we say that it is because light
travels at a finite velocity. But really, of course, it is because what we call the speed of light is simply the
ratio of space to time. One light year is equal to one year. And we see a universe as if outside of us by this
elaborate trick of seeing everything as back in time, and in just such a way that the total separation between
the perceiver and the perceived remains zero.
It is not clear that any Advaita Vedantin, in ancient time, understood clearly that space and time are opposites,
but it is clear that they understood that the separation between the perceiver and the perceived is zero. As Shankara
says in the first three verses of the Dakshinamurti Stotram:
"Seeing the universe existing within himself, like a city seen in a mirror, yet appearing as if produced
outside, through Maya or apparition, as in sleep . . . He who, through his own will, like a mighty magician or
some great yogi, spreads out this universe which exists indeterminate, like the germ of a seed, and is later on
diversified by the difference arising from the notion of space and time created by Maya .
He whose manifestation, the essence of which is reality, appears as the substance of fictitious notions, who is
the direct illumination of those who realize the identity of the perceiver and the perceived, and through the immediate
perception of whom there is no more return to the ocean of worldly existence, to Him, incarnate as the teacher,
to Him be this salutation."
|



